- These benchmarks compare the performance of matrix vector multiplies using MboNumOp to assembled sparse matrix vector multiplies. The assembled matrices correspond to regular compressed sparse row (CSR) matrices. This matrix format is sometimes referred to as Yale formate.
Performance model for assembled operator application
- Operator application for assembled matrices is typically memory bandwidth limited. For each complex multiply-add we need to load at least
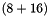 Byte. The first
Byte. The first 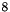 Byte are for the column index of the non-zero. The second
Byte are for the column index of the non-zero. The second 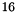 Byte are the complex number for the non-zero entry in the matrix. Note that this estimate assumes that the right hand side values are caches which is not always the case. 24B per multiply add is thus an optimistic estimate. It corresponds to an arithmetic intensity of
Byte are the complex number for the non-zero entry in the matrix. Note that this estimate assumes that the right hand side values are caches which is not always the case. 24B per multiply add is thus an optimistic estimate. It corresponds to an arithmetic intensity of 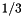 floating point operations per Byte. For a stream bandwidth of
floating point operations per Byte. For a stream bandwidth of 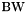 we get
we get 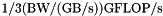 .
.
Performance model for MboNumOp
- The implementation of the matrix vector multiply inside of MboNumOp is going to evolve. Currently, this method is essentially streaming both source and destination vector for each simple operator. A simple operator in this context is a tensor product composed entirely of identities and individual sparse matrix entries. This means that the MboNumOp matrix vector multiply is largely memory bandwidth limited. In its current implementation we have an arithmetic intensity of
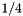 . The fact that this implementation is still slightly faster than the assembled matrix vector multiply despite being even more memory bandwidth bound is probably due to the more regular data access pattern. We avoid the indirect data accesses in the assembled matrix vector multiply.
. The fact that this implementation is still slightly faster than the assembled matrix vector multiply despite being even more memory bandwidth bound is probably due to the more regular data access pattern. We avoid the indirect data accesses in the assembled matrix vector multiply.
- Before we start we need to bring the Mbo library into scop by including several headers. We need the main Mbo.h header as well as MboVec.h
- In addition we need the following system headers
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <time.h>
#include <math.h>
- The following two functions are used to construct the MboNumOp's needed in this benchmark. They are defined further down.
static MboNumOp buildTavisCummingsHamiltonian(
int nAtoms,
int nPhotons);
- The following function builds all operators we're using for the comparison. Currently we're using the many particle angular momentum operator
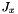 as well as the Tavis-Cummings Hamiltonian.
as well as the Tavis-Cummings Hamiltonian. numOps specifies the total number of operators that have been allocated in the ops array.
static void buildAllOps(
int numOps,
MboNumOp* ops)
{
int i;
static const int numPtclsJxMin = 8;
static const int numPtclsJxMax = 18;
for (i = numPtclsJxMin; i < numPtclsJxMax; ++i) {
if (numOps <= 0) return;
*ops = buildJx(i);
++ops;
--numOps;
}
for (i = 0; i < 10; ++i) {
if (numOps <= 0) return;
*ops = buildTavisCummingsHamiltonian(10 + i, 10);
++ops;
--numOps;
}
}
- The benchmarks are run by simply creating the operators and then invoking runBenchmark on each one of them.
int main() {
int numOps = 20, i;
ops = (
MboNumOp*)malloc(numOps *
sizeof(*ops));
buildAllOps(numOps, ops);
for (i = 0; i < numOps; ++i) {
runBenchmark(ops[i]);
}
Here we release all resources associated with the operators.
for (i = 0; i < numOps; ++i) {
}
free(ops);
}
- The CSR data structure defined in the following code is used to represent the assembled matrices.
dim is the dimension of the matrix; i is an array with the offsets for the different rows; j are the column indices of the non-zero entries; and a are the non-zero values.
- The following function initializes a CSR structure in a well defined state.
static struct CSR createCSR()
{
csr.i = 0;
csr.j = 0;
csr.a = 0;
return csr;
}
- The following function deallocates all memory in a CSR matrix.
static void destroyCSR(
struct CSR *csr)
{
free(csr->i);
free(csr->j);
free(csr->a);
}
getCSRMatrix creates the CSR matrix corresponding to a MboNumOp. This function uses mboNumOpRowOffsets and mboNumOpSparseMatrix to obtain the sparse matrix data. csr should have been previously created with createCSR.
{
csr->dim = dim;
csr->i = malloc((dim + 1) * sizeof(*csr->i));
csr->j = malloc(csr->i[dim] * sizeof(*csr->j));
csr->a = malloc(csr->i[dim] * sizeof(*csr->a));
}
BenchmarkData is a simple container for the results from a benchmark run. It is used to record the execution times of several runs, storage requirements, and the number of floating point operations.
int numIters;
double *times;
double storage;
double numFlops;
};
- A
struct BenchmarkData can be initialized with the following function
{
bm.numIters = numIters;
bm.times = malloc(numIters * sizeof(*bm.times));
bm.storage = 0;
bm.numFlops = 0;
return bm;
}
and it is destroyed with
- A CSR matrix can be applied to a vector by means of the following function.
{
for (row = 0; row < csr->dim; ++row) {
tmp.
re = beta.
re * y[row].
re - beta.
im * y[row].
im;
tmp.im = beta.
re * y[row].
im + beta.
im * y[row].
re;
for (i = csr->i[row]; i < csr->i[row + 1]; ++i) {
col = csr->j[i];
tmpp.re = csr->a[i].
re * alpha.
re - csr->a[i].
im *
tmpp.im = csr->a[i].
re * alpha.
im + csr->a[i].
im *
tmp.re += x[col].
re * tmpp.re - x[col].
im * tmpp.im;
tmp.im += x[col].
re * tmpp.im + x[col].
im * tmpp.re;
}
}
}
- This is a simple driver for timing the execution time of the matrix vector multiplication using assembled matrices. This driver simply invokes
applyCSRMatrix repeatedly and records the execution time.
{
struct CSR csr = createCSR();
MboVec x, y;
int i;
clock_t tstart, tend;
getCSRMatrix(op, &csr);
bm.numFlops = csr.i[csr.dim] * 8.0;
for (i = 0; i < numIters; ++i) {
tstart = clock();
applyCSRMatrix(alpha, &csr, xarr, beta, yarr);
tend = clock();
bm.times[i] = (double)(tend - tstart) / CLOCKS_PER_SEC;
}
destroyCSR(&csr);
return bm;
}
The driver for the MboNumOp's is completely analogous:
{
clock_t tstart, tend;
MboVec x, y;
int i;
for (i = 0; i < numIters; ++i) {
tstart = clock();
tend = clock();
bm.times[i] = (double)(tend - tstart) / CLOCKS_PER_SEC;
}
return bm;
}
- The average of several numbers is computed as follows. This can be used to get average run times for the different benchmarks.
static double average(const double *x, int n)
{
double avg = 0.0;
int i;
for (i = 0; i < n; ++i) {
avg += x[i];
}
return avg / (double)n;
}
- A pair of assembled/unassembled benchmarks is printed to the screen as follows
static void printBenchmarkReport(
struct BenchmarkData *assembledBM,
{
double meanTimeAssembled, meanTimeMbo;
double gflopsAssembled, gflopsMbo;
meanTimeAssembled = average(assembledBM->times, assembledBM->numIters);
meanTimeMbo = average(mboBenchmark->times, mboBenchmark->numIters);
gflopsAssembled = assembledBM->numFlops / meanTimeAssembled / 1.0e9;
gflopsMbo = assembledBM->numFlops / meanTimeMbo / 1.0e9;
printf("%1.2lf (%1.2Es) %1.2lf (%1.2Es) %1.2lfx ", gflopsMbo,
meanTimeMbo, gflopsAssembled, meanTimeMbo,
meanTimeAssembled / meanTimeMbo);
if (valid) {
printf("[PASSED]\n");
} else {
printf("[FAILED]\n");
}
}
- To compute the error we use the L2 norm of the difference between two vectors:
static double distance(MboVec x, MboVec y,
MboGlobInd d)
{
double dist = 0;
for (i = 0; i < d; ++i) {
diff.re = xarr[i].
re - yarr[i].
re;
diff.im = xarr[i].
im - yarr[i].
im;
dist += diff.re * diff.re + diff.im * diff.im;
}
dist = sqrt(dist);
return dist;
}
- The
verify method compares the results obtained from the assembled operators and the unassembled operators in the L2 norm. If the error is "small enough" we return a nonzero value to indicate success.
{
int valid = 0;
MboVec x, yMboNumOp, yAssembled;
struct CSR csr = createCSR();
double error;
Compute result with MboNumOp
Compute result with assembled operator
getCSRMatrix(op, &csr);
applyCSRMatrix(alpha, &csr, xarr, beta, yarr);
error = distance(yMboNumOp, yAssembled, dim) / sqrt((double)dim);
destroyCSR(&csr);
static const double TOLERANCE = 1.0e-10;
if (error > TOLERANCE) {
valid = 0;
} else {
valid = 1;
}
return valid;
}
- Running of the benchmarks, verification, and reporting for a given operator is orchestrated as follows:
{
static const int numIters = 2;
runAssembledBenchmark(op, numIters);
struct BenchmarkData mboBenchmark = runMboBenchmark(op, numIters);
int operatorValid = verify(op);
printBenchmarkReport(&assembledBenchmark, &mboBenchmark, operatorValid);
destroyBenchmarkData(&assembledBenchmark);
destroyBenchmarkData(&mboBenchmark);
}
- Resonance frequency of ith atom used in the construction of the Tavis-Cummings Hamiltonian below. This is an entirely arbitrary choice
static double omega(int i)
{
return 1.3 * i;
}
- Finally, the last two functions are used to construct the operators in the benchmark.
MboNumOp buildTavisCummingsHamiltonian(
int nAtoms,
int nPhotons)
{
MboTensorOp inhomogeneousJz, jPlus, jMinus, idField, idAtoms, A, Ad, N,
H, *factors;
int i;
build various Hilbert spaces
for (i = 0; i < nAtoms; ++i) {
}
build atomic operators
for (i = 0; i < nAtoms; ++i) {
tmp.re = omega(i);
tmp.im = 0;
}
for (i = 0; i < nAtoms; ++i) {
}
for (i = 0; i < nAtoms; ++i) {
}
build field operators
The frequency of the cavity
tmp.re = 2.7;
tmp.im = 0;
Assemble Hamiltonian
factors = malloc(2 * sizeof(*factors));
factors[0] = idField;
factors[1] = inhomogeneousJz;
factors[0] = N;
factors[1] = idAtoms;
factors[0] = A;
factors[1] = jPlus;
factors[0] = Ad;
factors[1] = jMinus;
free(factors);
assert(err == MBO_SUCCESS);
Release all resources
return H_compiled;
}
{
int i;
build various Hilbert spaces
for (i = 0; i < nAtoms; ++i) {
}
build atomic operators
for (i = 0; i < nAtoms; ++i) {
tmp.re = 0.5;
tmp.im = 0;
}
assert(err == MBO_SUCCESS);
Release all resources
Plain source code
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <time.h>
#include <math.h>
static MboNumOp buildTavisCummingsHamiltonian(
int nAtoms,
int nPhotons);
static void buildAllOps(
int numOps,
MboNumOp* ops)
{
int i;
static const int numPtclsJxMin = 8;
static const int numPtclsJxMax = 18;
for (i = numPtclsJxMin; i < numPtclsJxMax; ++i) {
if (numOps <= 0) return;
*ops = buildJx(i);
++ops;
--numOps;
}
for (i = 0; i < 10; ++i) {
if (numOps <= 0) return;
*ops = buildTavisCummingsHamiltonian(10 + i, 10);
++ops;
--numOps;
}
}
int main() {
int numOps = 20, i;
ops = (
MboNumOp*)malloc(numOps *
sizeof(*ops));
buildAllOps(numOps, ops);
for (i = 0; i < numOps; ++i) {
runBenchmark(ops[i]);
}
for (i = 0; i < numOps; ++i) {
}
free(ops);
}
};
static struct CSR createCSR()
{
csr.i = 0;
csr.j = 0;
csr.a = 0;
return csr;
}
static void destroyCSR(
struct CSR *csr)
{
free(csr->i);
free(csr->j);
free(csr->a);
}
{
csr->dim = dim;
csr->i = malloc((dim + 1) * sizeof(*csr->i));
csr->j = malloc(csr->i[dim] * sizeof(*csr->j));
csr->a = malloc(csr->i[dim] * sizeof(*csr->a));
}
int numIters;
double *times;
double storage;
double numFlops;
};
{
bm.numIters = numIters;
bm.times = malloc(numIters * sizeof(*bm.times));
bm.storage = 0;
bm.numFlops = 0;
return bm;
}
{
free(bm->times);
}
{
for (row = 0; row < csr->dim; ++row) {
tmp.
re = beta.
re * y[row].
re - beta.
im * y[row].
im;
tmp.im = beta.
re * y[row].
im + beta.
im * y[row].
re;
for (i = csr->i[row]; i < csr->i[row + 1]; ++i) {
col = csr->j[i];
tmpp.re = csr->a[i].
re * alpha.
re - csr->a[i].
im *
tmpp.im = csr->a[i].
re * alpha.
im + csr->a[i].
im *
tmp.re += x[col].
re * tmpp.re - x[col].
im * tmpp.im;
tmp.im += x[col].
re * tmpp.im + x[col].
im * tmpp.re;
}
}
}
{
struct CSR csr = createCSR();
MboVec x, y;
int i;
clock_t tstart, tend;
getCSRMatrix(op, &csr);
bm.numFlops = csr.i[csr.dim] * 8.0;
for (i = 0; i < numIters; ++i) {
tstart = clock();
applyCSRMatrix(alpha, &csr, xarr, beta, yarr);
tend = clock();
bm.times[i] = (double)(tend - tstart) / CLOCKS_PER_SEC;
}
destroyCSR(&csr);
return bm;
}
{
clock_t tstart, tend;
MboVec x, y;
int i;
for (i = 0; i < numIters; ++i) {
tstart = clock();
tend = clock();
bm.times[i] = (double)(tend - tstart) / CLOCKS_PER_SEC;
}
return bm;
}
static double average(const double *x, int n)
{
double avg = 0.0;
int i;
for (i = 0; i < n; ++i) {
avg += x[i];
}
return avg / (double)n;
}
static void printBenchmarkReport(
struct BenchmarkData *assembledBM,
{
double meanTimeAssembled, meanTimeMbo;
double gflopsAssembled, gflopsMbo;
meanTimeAssembled = average(assembledBM->times, assembledBM->numIters);
meanTimeMbo = average(mboBenchmark->times, mboBenchmark->numIters);
gflopsAssembled = assembledBM->numFlops / meanTimeAssembled / 1.0e9;
gflopsMbo = assembledBM->numFlops / meanTimeMbo / 1.0e9;
printf("%1.2lf (%1.2Es) %1.2lf (%1.2Es) %1.2lfx ", gflopsMbo,
meanTimeMbo, gflopsAssembled, meanTimeMbo,
meanTimeAssembled / meanTimeMbo);
if (valid) {
printf("[PASSED]\n");
} else {
printf("[FAILED]\n");
}
}
static double distance(MboVec x, MboVec y,
MboGlobInd d)
{
double dist = 0;
for (i = 0; i < d; ++i) {
diff.re = xarr[i].
re - yarr[i].
re;
diff.im = xarr[i].
im - yarr[i].
im;
dist += diff.re * diff.re + diff.im * diff.im;
}
dist = sqrt(dist);
return dist;
}
{
int valid = 0;
MboVec x, yMboNumOp, yAssembled;
struct CSR csr = createCSR();
double error;
getCSRMatrix(op, &csr);
applyCSRMatrix(alpha, &csr, xarr, beta, yarr);
error = distance(yMboNumOp, yAssembled, dim) / sqrt((double)dim);
destroyCSR(&csr);
static const double TOLERANCE = 1.0e-10;
if (error > TOLERANCE) {
valid = 0;
} else {
valid = 1;
}
return valid;
}
{
static const int numIters = 2;
runAssembledBenchmark(op, numIters);
struct BenchmarkData mboBenchmark = runMboBenchmark(op, numIters);
int operatorValid = verify(op);
printBenchmarkReport(&assembledBenchmark, &mboBenchmark, operatorValid);
destroyBenchmarkData(&assembledBenchmark);
destroyBenchmarkData(&mboBenchmark);
}
static double omega(int i)
{
return 1.3 * i;
}
MboNumOp buildTavisCummingsHamiltonian(
int nAtoms,
int nPhotons)
{
MboTensorOp inhomogeneousJz, jPlus, jMinus, idField, idAtoms, A, Ad, N,
H, *factors;
int i;
for (i = 0; i < nAtoms; ++i) {
}
for (i = 0; i < nAtoms; ++i) {
tmp.re = omega(i);
tmp.im = 0;
}
for (i = 0; i < nAtoms; ++i) {
}
for (i = 0; i < nAtoms; ++i) {
}
tmp.re = 2.7;
tmp.im = 0;
factors = malloc(2 * sizeof(*factors));
factors[0] = idField;
factors[1] = inhomogeneousJz;
factors[0] = N;
factors[1] = idAtoms;
factors[0] = A;
factors[1] = jPlus;
factors[0] = Ad;
factors[1] = jMinus;
free(factors);
assert(err == MBO_SUCCESS);
return H_compiled;
}
{
int i;
for (i = 0; i < nAtoms; ++i) {
}
for (i = 0; i < nAtoms; ++i) {
tmp.re = 0.5;
tmp.im = 0;
}
assert(err == MBO_SUCCESS);
return Jx_compiled;
}
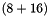 Byte. The first
Byte. The first 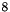 Byte are for the column index of the non-zero. The second
Byte are for the column index of the non-zero. The second 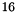 Byte are the complex number for the non-zero entry in the matrix. Note that this estimate assumes that the right hand side values are caches which is not always the case. 24B per multiply add is thus an optimistic estimate. It corresponds to an arithmetic intensity of
Byte are the complex number for the non-zero entry in the matrix. Note that this estimate assumes that the right hand side values are caches which is not always the case. 24B per multiply add is thus an optimistic estimate. It corresponds to an arithmetic intensity of 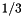 floating point operations per Byte. For a stream bandwidth of
floating point operations per Byte. For a stream bandwidth of 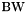 we get
we get 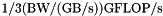 .
.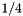 . The fact that this implementation is still slightly faster than the assembled matrix vector multiply despite being even more memory bandwidth bound is probably due to the more regular data access pattern. We avoid the indirect data accesses in the assembled matrix vector multiply.
. The fact that this implementation is still slightly faster than the assembled matrix vector multiply despite being even more memory bandwidth bound is probably due to the more regular data access pattern. We avoid the indirect data accesses in the assembled matrix vector multiply.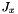 as well as the Tavis-Cummings Hamiltonian.
as well as the Tavis-Cummings Hamiltonian.  1.8.8
1.8.8